Proyecto Origami

I. Simbología

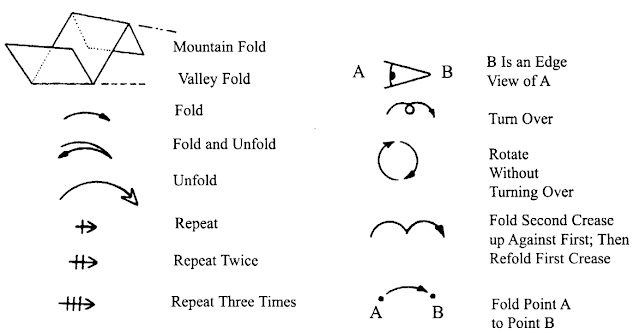
Para poder desarrollar el origami modular es conveniente primero conocer su simbología

 

II. Construcciones básicas

Antes de iniciar con los módulos practiquemos primero la simbología mediante las construcciones básicas mas importantes del origami modular, las cuales son:

II.1. Dividir el lado de un cuadrado en tres partes iguales.
  

II.2. Construir un triángulo equilátero a partir de un cuadrado.

II.3. Construir un pentágono regular a partir de un cuadrado.

II.4. Construir un hexágono regular a partir de un cuadrado.

 

II.5. Construir un octágono regular a partir de un cuadrado.

 

III. Módulo Sonobe básico

El módulo Sonobe que utilizaremos para construir el cubo, el octaedron y el icosaedron, se encuentra en el libro Modular Origami Polyhedra de los autores Lewis Simon, Bennett Arnstein y Rona Gurkewitz. Ahora, con mucho cuidado sigue los siguientes pasos, marcando muy bien cada quiebre para que tu módulo Sonobe quede perfectamente definido:

Ya tienes en tus manos tu primer módulo. Cada módulo posee dos alas y dos bolsillo cortos en el que entran las alas de otros módulos. Para facilitar el ensamble de los poliedros, debes primero formar una espina que deberá verse ası́:

III.1. Para construir el cubo es necesario ensamblar seis módulos o dos espinas:

III.2. Mientras que en el octaedron se ensamblan doce módulos formando un vértice de cuatro espinas como primer paso:

III.3. Por último, debes usar treinta módulos para el icosaedron formando un vértice de cinco espinas como base para construir el poliedro:

 

IV. Módulo Triangular de Arista

El módulo triangular de arista se utiliza para construir el tetraedro, el octaedro y el icosaedro. Este módulo también lo podemos encontrar en el libro Modular Origami Polyhedra. Para su construcción debes disponer de un rectángulo cuyo largo es el doble de su ancho. Ahora, sigue los siguientes pasos marcando muy bien cada quiebre para que tu módulo quede perfectamente definido:

Al igual que el módulo Sonobe este posee dos alas y dos bolsillo en el que entran las alas de otros módulos. Para facilitar el ensamble de los poliedros, debes hacer lo siguiente:

IV.1 Formar un vértice de tres módulos (o aristas) en el caso del tetraedro para ensamblar un total de seis módulos
 

IV.2. Una vértice de cuatro módulos (o aristas) para el octaedro y ensamblar un total de doce módulos:
 

IV.3. Finalmente, debes formar un vértice de cinco módulos (o aristas) para el icosaedro y ensamblar un total de treinta módulos
 

 

V. Módulo Pentagonal de 108 grados

El módulo pentagonal que utilizaremos para construir el dodecaedro, también se encuentra en el libro Modular Origami Polyhedra ya mencionado. Ahora, con mucho cuidado sigue los siguientes pasos, marcando muy bien cada quiebre para que tu módulo quede perfectamente definido:

Como es costumbre en el origami modular este módulo posee dos alas y dos bolsillo en el que entran las alas de otros módulos. Para facilitar el ensamble del poliedro, debes primero formar un vértice que deberá verse así:

Una vez tengas treinta módulos puedes proceder a construir el dodecaedro tal como se puede apreciar en la siguiente fotografía:

 

VI. Módulo Giroscopio cuadrado

Este tipo de módulos está conformado por dos piezas entrelazadas como se puede apreciar en la tercera instrucción. Cada pieza está hecha de un polígono construible de la sección II. A continuación se presentan las instrucciones para construir un módulo giroscopio cuadrado. No olvides marcar muy bien cada quiebre para que tu módulo quede perfectamente definido:

VI.1. Usando seis módulos se puede construir el octaedro esqueleto o giroscopio, llamado así por Lewis porque uno pequeño se puede hacer girar en la palma de la mano como un trompo.

 

VII. Módulo Giroscopio Triangular

Este módulo está conformado por dos piezas entrelazadas como se puede apreciar en la tercera instrucción, donde cada pieza es un triángulo equilátero. A continuación se presentan los pasos para construir el módulo giroscopio triangular:

 

Bibliografía

• Lewis Simon, Bennett Arnstein and Rona Gurkewitz. Modular Origami Polyhedra. Dover publications, INC. Mineola, New York.
• Meenakshi Mukerji. Marvelous Modular Origami. A K Peters, Ltd. Natick, Massachusetts.
• Rona Gurkewitz and Bennett Arnstein. 3-D Geometric Origami Modular Polyhedra. Dover publications, INC. New York.